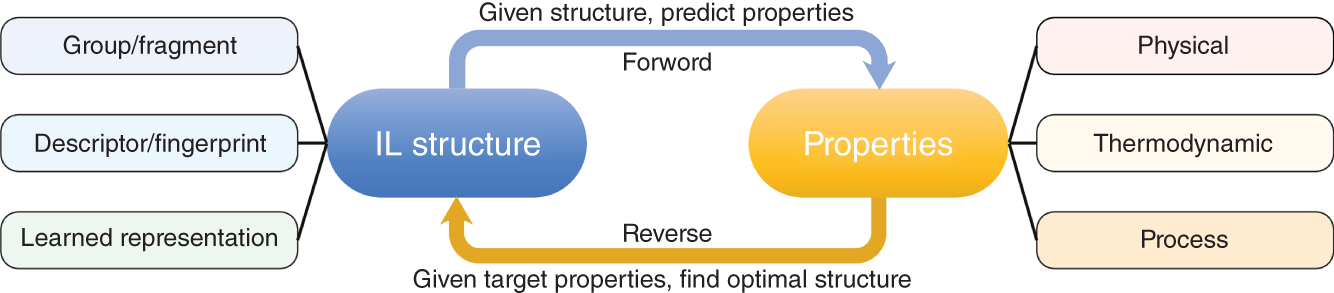
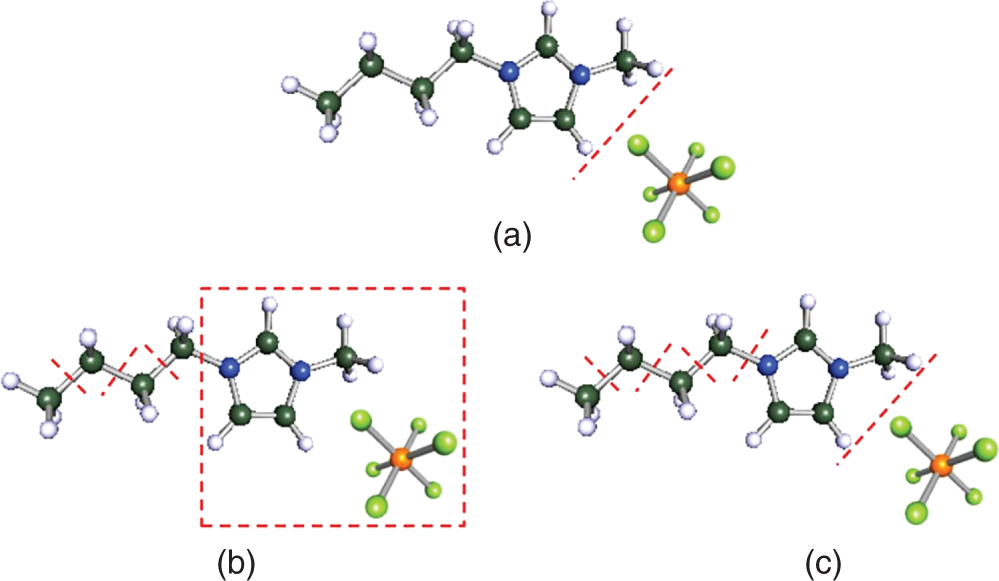
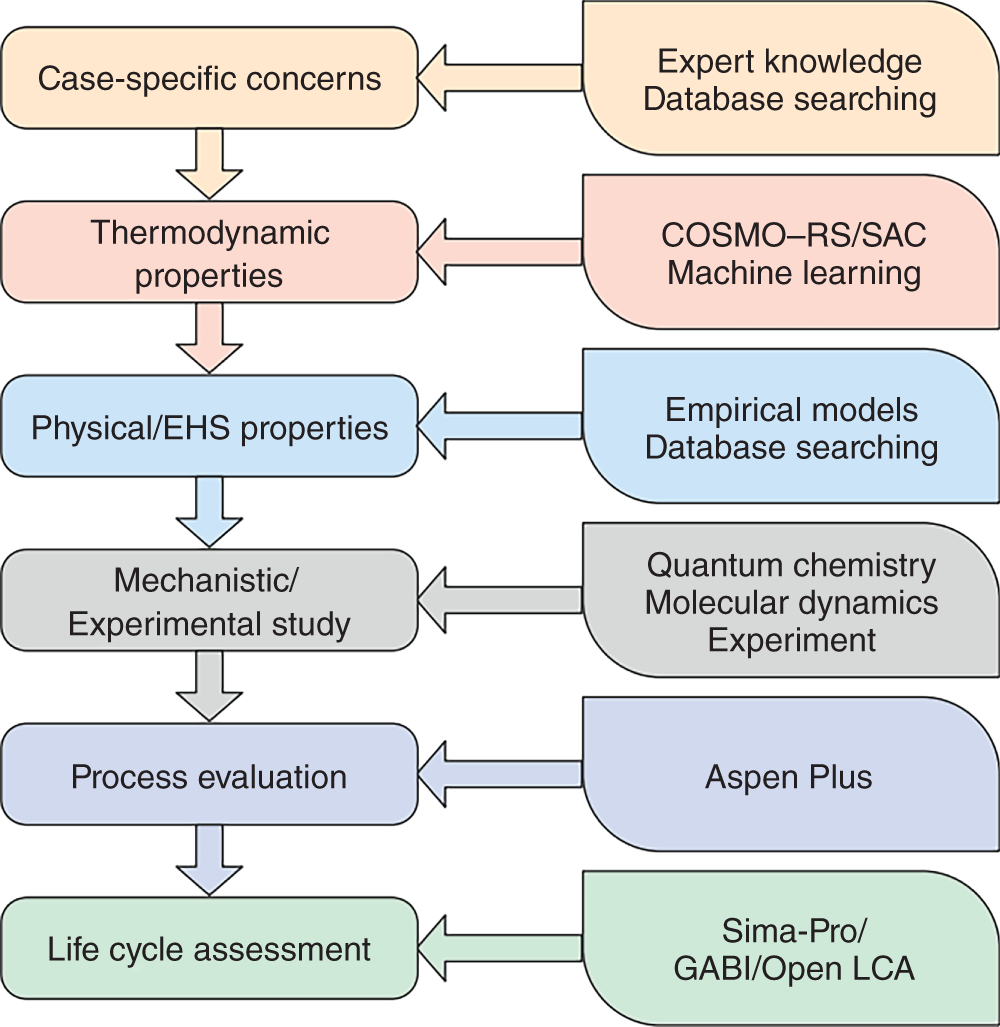
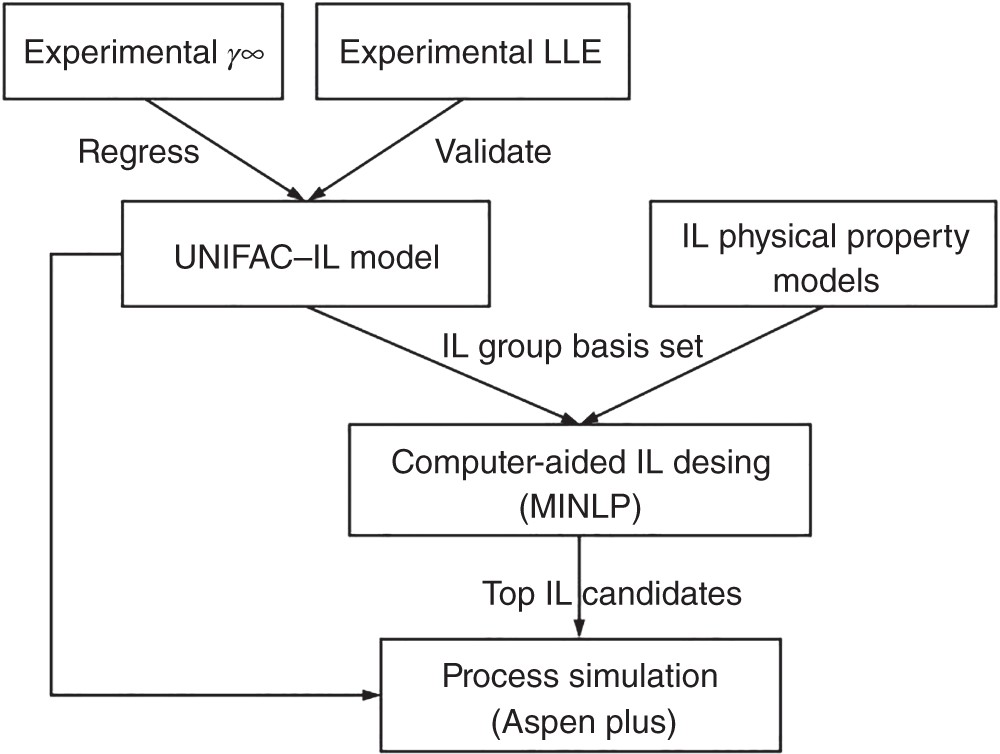
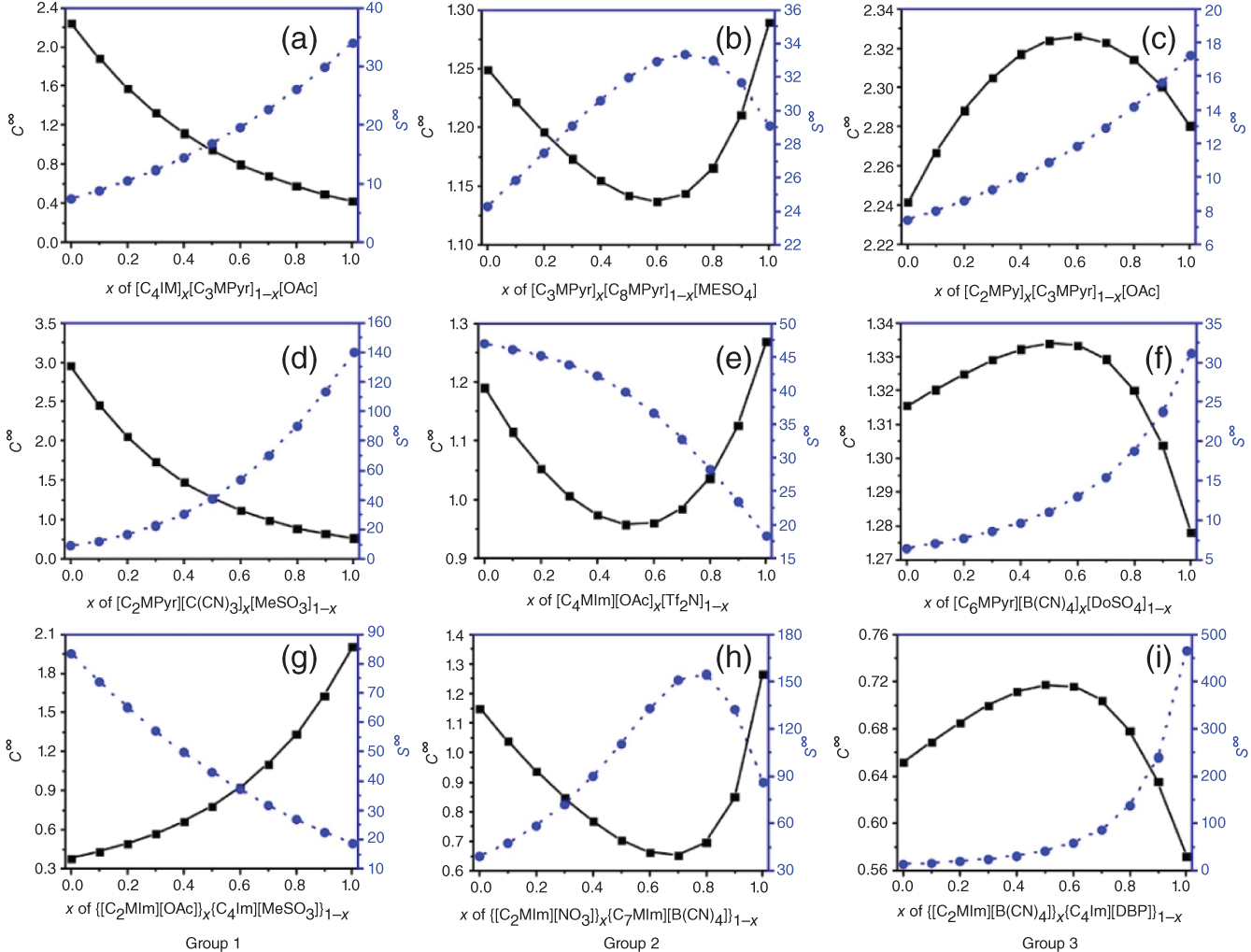
Ruofan Gu and Zhen Song State Key Laboratory of Chemical Engineering, School of Chemical Engineering, East China University of Science and Technology, 130 Meilong Road, Shanghai 200237, China Ionic liquids (ILs) are commonly acknowledged as prospective substitutes for organic solvents because of their distinctive physicochemical features such as negligible vapor pressure, broad liquidus window, nonflammability, high thermal and chemical stability, high ionic conductivity, selectively strong solvating ability toward many different chemicals, etc. [1]. The properties of ILs are widely customizable to fit task-specific requirements through deliberate combinations of cation, anion, and substituents [2–4]. They have been extensively explored in many chemical separation processes like extractive distillation (ED), liquid–liquid extraction, and gas absorption [5–9]. For a particular separation task, it is crucial to know the phase equilibrium behavior and identify an appropriate IL among numerous different ILs with unique properties. However, such a selection of ILs, as the key decision for the design of a specific IL-based process, still relies heavily on experimental testing of a small number of candidates in most cases. Considering the wide variety of possible IL structures and potential applications, experimental methods for screening ILs are labor-intensive, expensive, time-consuming, and not even realistic to screen the optimal IL candidate. Hence, proper theoretical methods to model the thermodynamic properties of ILs and IL-based separation systems are highly required to aid in selecting the best ILs for particular tasks. In contrast to conventional organic molecules, ILs are a unique class of compounds composed entirely of anions and cations (in most cases, large asymmetric organic cations and organic/inorganic anions). Consequently, a great deal of effort has been invested in IL structure–property modeling and molecular design methodology. As the combinations of cations, anions, and substituents are virtually unlimited, it is particularly suitable to apply the computer-aided molecular design (CAMD) approach to IL design, i.e. computer-aided ionic liquid design (CAILD). In recent years, CAILD-related studies have increased considerably in literature. On the one hand, IL structure–property models including physical and thermodynamic properties as well as some properties related to environment, health, and safety (EHS) or sustainability have exploded due to the increase in the amount of available data and/or the growing popularity of advanced modeling methods (e.g. machine learning, ML). In addition, the CAMD approach has also been extended to cover IL mixtures (also known as double-salt ionic liquids [DSILs]). Our group has also conducted substantial research on the above aspects, and this chapter will briefly summarize the main direction of ML-boosted rational screening of task-specific ILs. The whole chapter is organized as follows. Section 3.2 presents molecular representations of ILs, and following that, Section 3.3 describes the research on ML-based structure–property models. Section 3.4 describes some representative applications of ML-assisted rational screening of ILs for specific tasks. Finally, Section 3.5 briefly summarizes this chapter and makes some future perspectives in the field. In general, CAILD aims to efficiently select IL from a large number of potential chemical structures to meet specific task requirements. Similar to the well-known concept of CAMD, CAILD can also be divided into two subproblems (see Figure 3.1). The forward subproblem involves linking the molecular structure of IL with its properties through a structure–property model. In this case, a specific term, quantitative structure–property relationship (QSPR), can be widely referred to. These structural property models can be based on diverse molecular representations such as groups or fragments, molecular descriptors or fingerprints, and machine-learned representations. The reverse subproblem is to determine the IL structure that can provide the optimal value of target properties (such as physical, thermodynamic, and process) based on the established structure–property models. When conducting CAILD, if a known IL database is prespecified, the term “screening” can be used, meaning to search for the best IL candidate from the existing structural space. However, new cation–anion combinations that have not been experimentally synthesized or reported can still be identified and can be considered as new IL. The term “design” can be used to potentially identify IL with novel cationic and/or anionic structures based on the virtual combinations of smaller IL substructures such as groups or fragments. As in the CAILD scheme above, the scope of application of IL structure–property modeling directly determines the molecular space that can be explored by the CAILD method. Thus, a reliable IL structure–property model is a prerequisite for enabling computer-aided IL screening or design. Two key pillars in structure–property modeling are the proper molecular representation of ILs and the modeling algorithm. Different molecular representations of ILs can be employed, such as groups or fragments, molecular descriptors or fingerprints derived from cheminformatics or quantum chemical calculations, as well as learned representations. Accordingly, various modeling algorithms can be considered for pairing the IL representations, ranging from classical linear algorithms to nonlinear algorithms and deep learning (DL) algorithms. It is worth mentioning that the development or extension of some physically based models, such as UNIFAC (universal quasichemical functional-group activity coefficients) and COSMO (conductor-like screening model) types of activity coefficient models follows the corresponding theoretical foundations and does not involve different modeling algorithms. However, from the molecular representations point of view, UNIFAC models belong to molecular group-based structure–property models, whereas COSMO-type activity coefficient models essentially belong to structure–property models based on quantum chemical molecular fingerprints. Therefore, the foundations of different molecular representations will be briefly introduced in this section. Figure 3.1 Scheme of the forward and reverse subproblems in CAILD. Just like the property modeling of conventional molecules, the use of groups or fragments as molecular representations is a fundamental and commonly employed approach for modeling the properties of ILs and IL-related systems. Among the models that rely on such molecular representations, the group contribution (GC) method is a well-established framework. This method adheres to the additivity rule, postulating that the properties of a given molecule can be approximated by summing the contributions of its constituent groups, typically composed of a few atoms and bonds. Within the context of group decomposition for ILs, three distinct approaches are generally employed, as illustrated in Figure 3.2: (a) decomposing into one cation and one anion, (b) decomposing into multiple groups while treating the cation skeleton and the anion as unified entities, and (c) decomposing into several groups with separate treatment of the cation skeleton. Figure 3.2 Three different approaches to decompose ILs into UNIFAC functional groups (illustrated with [C4MIm][PF6]). Source: Song et al. [10]/with permission of John Wiley & Sons. Among the three approaches, the first method necessitates the inclusion of parameters associated with each potential cation and anion, limiting its coverage to specific cation–anion combinations. The second approach can accommodate the influence of cation substituents and avoid the use of the charged groups, which is sometimes considered theoretically advantageous, as adopted in the UNIFAC model extension proposed by Lei et al. [11]. The third approach is the most widely adopted for modeling IL properties due to its superior adaptability in capturing structural variations in cations, anions, and substituents. This approach offers the broadest applicability and flexibility during the CAILD stage. For instance, (i) Chen et al. [12] employed the third group decomposition to develop GC models for IL properties, namely density, heat capacity, viscosity, surface tension, and melting point. (ii) Song et al. [10, 13] extended the original UNIFAC models to encompass IL-solute systems, resulting in an extensive parameter matrix for the UNIFAC–IL model. In the domain of ILs property modeling, it is observed that the group or fragment-based modeling approach is, to an extent, influenced by the experience and choices of researchers. Such variability in GC schemes presents challenges in the implementation of CAILD. Specifically, researchers may need to simultaneously navigate multiple group decomposition strategies to achieve effective molecular encoding. In this context, ambiguities in group decomposition can sometimes lead to misconceptions among model users, subsequently affecting the predictive accuracy of the models [14]. Moreover, it is imperative to strike a balance between simplicity and predictive accuracy when defining the groups or fragments for IL property modeling. Opting for a smaller number of functional groups may make molecular representation simpler, but it often undermines the accuracy of predictions. Conversely, incorporating a larger number of groups, reaching the complexity of molecular levels, amplifies the dimensional breadth of the molecular representation. This enhanced dimensionality reflects the proximal effects and interactions between groups more accurately, thereby augmenting the model’s predictive or at least correlative performance. However, it is crucial to note that the development of such methodologies typically depends on extensive property datasets. Currently, only a few IL properties, such as density, viscosity, and CO2 solubility, have been extensively studied experimentally, allowing for the application of these high-accuracy predictive models. Despite the relative simplicity of implementing GC models in the CAMD of ILs, they also exhibit certain limitations. First, not all properties adhere to the simple additive rule. Second, these models’ fundamental assumptions overlook the proximal effects of groups within molecules and are unable to differentiate between structures with varying connectivity. To address these limitations, enhancements in the property modeling of conventional molecules have been introduced, including the incorporation of multiple-order groups (first-, second-, and/or third-order groups, also known as the GC+ approach) or additional interaction terms [15, 16]. Nevertheless, the advancement of such models for IL properties remains limited to date, partly attributable to the relatively small size of the datasets available [17, 18]. The use of fingerprints based on the COSMO theory, particularly those utilizing the screening charge density (SCD or σ) distribution, has demonstrated notable potential in the area of molecular property modeling. This type of molecular fingerprint can quantitatively represent information such as polarity and hydrogen bond accepting/donating capabilities. Specifically, the COSMO calculations based on quantum chemical provide a discrete surface for a molecule embedded in a virtual conductor, where each surface segment is characterized by its area ai and σi, taking into account the electrostatic screening around the molecule and the back polarization of the molecule [19]. The SCD distribution, commonly referred to as the σ-profile, represents the probability distribution of σi on each segment i [20, 21]. Although initially designed to link microscopic surface-interaction energies to macroscopic thermodynamic properties (i.e. as the input for COSMO–RS (conductor-like screening model for real solvent) thermodynamic calculations), σ-profiles have also been proven to be an effective fingerprint for property modeling [22–26]. In the realm of COSMO-derived fingerprints and descriptors, they have been successfully applied to the prediction of IL properties. For instance, (i) Palomar et al. [27] calculated the Sσ-profile descriptors for 45 imidazolium-based ILs, establishing a strong correlation with molecular volume and density (R2 > 0.99), demonstrating that the Sσ-profile is an effective representation method for ILs. (ii) Zhao et al. [28] utilized the Sσ-profile to predict the heat capacity of 46 ILs, encompassing a dataset of 2416 data points. Combined with the extreme learning machine algorithm, the resulting model showed reasonable performance in predicting heat capacity, with an average absolute relative deviation (AARD) of 0.60%. It is noteworthy that COSMO-derived molecular fingerprints or descriptors are contingent on the calculations of σ-profile and σ-potential; in their absence, quantum chemical calculations are required initially. Many of the above molecular representations have easily interpretable meanings that can support the interpretation of the models developed from them. However, there are also limitations of such molecular representations: (i) the descriptors are limited by the available knowledge space and (ii) the fingerprints are generally of large lengths when the dataset has a large variety, which leads to a large number of sparse vectors and affects model training. Learned molecular representations are gaining popularity in the field of predicting molecular properties. One approach is based on sequence modeling, where chemical structures are efficiently transformed into strings using simplified molecular-input line-entry system (SMILES) or the international chemical identifiers (InChIs). Chen et al. [29] recently extended the application of the SMILES transformer to enable the prediction of σ-profile as well as the VCOSMO of conventional molecules. First, the transformer model was pretrained on the ChEMBL25 database with 1 768 081 molecules using an encoder–decoder architecture that can effectively capture molecular fingerprints from the canonical SMILES of molecules. A convolutional neural network (CNN) model was trained and tested for predicting the σ-profile and VCOSMO on the VT-2005 database by employing the pretrained molecular fingerprints. The transformer–CNN model demonstrates significantly improved performance compared to the GC–COSMO approach. Recently, a similar framework called ILTransR [30] has been successfully developed for predicting 11 IL properties. It was pretrained on 10 243 410 IL-like SMILES and fine-tuned corresponding to each small, labeled IL property dataset. Another type of learned representation for molecules is based on the neural network entity embeddings [31]. Entity embedding can place similar entities closer together in the embedding space by mapping high-dimensional categorical variables to a low-dimensional learned representation. Research shows that when data are sparse and statistical information is unknown, entity embedding helps neural networks better generalize. Recently, Chen et al. [32] employed the neural network entity embeddings as the molecule representation method to develop the neural recommender system (RS) for predicting activity coefficients of IL-involved systems. Specifically, the neural network entity embedding was used to map each solute and each IL to a 128-number latent vector. The inner product or the cosine of the angle between latent vectors can assess the latent similarity of each IL and each solute. If one-hot-encoding is used for ILs and solutes, there would be a vector with the same dimensions as the number of ILs and solutes, where a “1” denotes a specific IL or solute and all other elements in the vector are “0.” In this way, vectors representing similar ILs or solutes are not “closer.” In contrast, it is possible to represent all ILs and solutes in smaller dimensions while mapping similar ILs and solutes closer together in the embedding space by training a neural network to learn entity embeddings. Entity embeddings can be learned as part of a neural network that predicts γ∞, with the embedding layer weights adjusted during training to minimize losses on the prediction problem. Based on COSMO, two models of activity coefficient have emerged: one for realistic solvents known as COSMO–RS [33] and the other for COSMO segment activity coefficient known as COSMO–SAC [34, 35]. These two models share a similar methodological framework but differ in the approach to handling the combinatorial and residual contributions in chemical property calculations. As both models require only the σ-profile and VCOSMO derived from quantum chemistry as input, they have been widely evaluated and used to predict the thermodynamic properties of IL-involved systems. Coutinho’s research group [36, 37] extensively evaluated the predictive performance of COSMO–RS for the liquid–liquid equilibrium (LLE) of over 150 binary and 180 ternary {IL + aromatic hydrocarbon + aliphatic hydrocarbon} systems, concluding that COSMO–RS mainly provides qualitative and semiquantitative trends in the phase behavior dependence of ILs and hydrocarbon molecules. The predictive performance of COSMO–RS has also been extensively evaluated for vapor–liquid equilibrium (VLE) and LLE of binary {IL + molecular compound} systems, as well as the mutual solubility of water and ILs. For example, to develop efficient separation processes (such as ED) based on ILs, it is necessary to understand the VLE behavior related to ILs. As experimental measurements are often time-consuming and expensive, reliable VLE prediction models are highly desired. Qin et al. [38] systematically evaluated the predictive performance of COSMO–RS for ternary and binary VLE systems containing ILs, with a large experimental database established, including 6531 ternary and 2265 binary systems. The VLE systems were divided into five ternary system subsets and three binary system subsets based on the type of solute molecule. The performance of COSMO–RS in capturing the effects of IL structure, solute structure, IL concentration, and temperature on VLE was also analyzed. COSMO–RS provides an overall qualitative description of VLE behavior and, in some cases, a quantitative description, making it a valuable tool for IL screening and process analysis related to the separation processes. The solubility of water and environmentally friendly solvent ILs is crucial for proper IL selection in chemical reactors and separation processes. Zhou et al. [39] predicted the mutual solubility of water and 1500 ILs (50 cations and 30 anions) at 298.15 K, using the COSMO–RS as a thermodynamic model. Based on the COSMO–RS calculations, the influence of cation and anion types, side chains, and substituent groups on water solubility was extensively analyzed, providing a pre-screening of candidate solvent ILs. Additionally, to gain a deeper understanding of their inherent solubility behavior, multiple water–IL interaction energies were calculated based on COSMO–RS calculations, comparing different types of molecular interactions between ILs and water in solution. It was confirmed that hydrogen bonding interactions between anions and water molecules have a major impact on solubility. Finally, to rapidly estimate solubility and select solvents, molecular descriptors were calculated for typical anions and anion families derived from COSMO–RS, indicating the strength of hydrogen bond acceptors on anions. Considering the quantum chemistry calculation of σ-profile is the most computationally expensive part of COSMO-type activity coefficient calculations; there have been attempts to generate σ-profiles without quantum chemical calculations, e.g. developing GC or ML methods based on existing σ-profile databases. For instance, (i) Peng et al. [40] proposed a CAILD method for designing IL solvents for specific separation processes, wherein they established a GC–COSMO method for estimating the σ-profile and cavity volume of cations of ILs. (ii) Zhang et al. [41] proposed a modified GC method, the COSMO–GC–IL method, for the quick prediction of IL σ-profiles and VCOSMO based on the σ-profile of the IL groups in their reference state as well as the two modification parameters. The effect of the molecular environment on the target group can be well described, allowing for the differentiation of the IL isomers. They validated the method by calculating the activity coefficients of 28 644 binary systems and 3410 ternary mixtures in LLE, using the σ-profiles and VCOSMO generated by the present method and the Dmol3 database, demonstrating the reliability of the COSMO–GC–IL method. (iii) As for the combination with the ML method, Chen et al. [29] have developed a DL method for quickly predicting the σ-profiles and VCOSMO of molecules. Molecular fingerprints can be obtained from the encoder state of the pretrained transformer model on the ChEMBL database, allowing for transfer learning from large-scale unlabeled data and improving generalization performance. They trained and tested a CNN model for the σ-profiles and VCOSMO on the VT-2005 database using the pretrained molecular fingerprints. The obtained transformer–CNN model notably outperforms the GC–COSMO method, predicting σ-profiles and VCOSMO of millions of molecules in just a few minutes. Of course, this promising method can be extended for the prediction of σ-profiles and VCOSMO of cations and anions of ILs, provided that a considerable database of σ-profiles and VCOSMO of ILs is available. The UNIFAC model is an efficient and practical thermodynamic prediction model based on GC methods. By knowing the groups in the mixture and the related group parameters, it can accurately calculate the activity coefficient of molecules in the system. Currently, the UNIFAC models for IL-involved systems (also known as the UNIFAC–IL model) have successfully fitted a large number of interaction parameters in the literature and have been widely used in IL screening or design for many typical separation processes. By adopting the group decomposition method in Figure 3.2c, Song et al. [10] successfully extended the UNIFAC model to the extraction of desulfurization systems. They used thiophene, alkanes (hexane, heptane, octane), aromatics (benzene, toluene, ethylbenzene), and cycloalkanes (cyclopentane, cyclohexane, cycloheptane) to regress UNIFAC interaction parameters between solute groups and IL groups based on experimental γ∞. This included 7 cation skeleton groups, 13 anion groups, and 7 conventional groups. They explicitly provided the AARD between experimental γ∞ and model-calculated γ∞ for various solutes, followed by external validation by predicting the LLE behavior of 171 systems. The low AARD values during γ∞ calculations and small root-mean-square deviation (RMSD) during LLE predictions fully demonstrate the reliability of the obtained model. Inspired by this encouraging result, they subsequently proposed a larger extension. They compiled a dataset of experimental γ∞ data for 83 molecular solutes in 214 ILs, totaling 39 358 data points. These 83 solutes included various types of conventional molecular species such as alkanes, cycloalkanes, aromatics, olefins, ketones, alcohols, ethers, ketones, sulfur compounds, nitrogen compounds, and water, while the 214 ILs were from 9 cation families and 29 anion families. Therefore, the UNIFAC–IL extension results covered 21 conventional main groups, 9 cation skeleton groups, and 29 anion groups. Due to the fact that ILs were divided into independent cation skeletons, anions, and substituent groups, the UNIFAC–IL model could cover most ILs, and molecular solutes involved in relevant studies. Meanwhile, they also provided the AARD between experimental and calculated γ∞ for various solutes and predicted a total of 860 ternary LLE systems and 99 ternary VLE systems for verification. These analyses demonstrate the predictive performance of the UNIFAC–IL model for different types of systems. From the above extension of UNIFAC based on experimental data, it can be seen that due to the shortage and uneven distribution of available data, there are still a large number of missing parameters in the parameter matrix. To overcome this limitation, Song et al. [13] systematically evaluated the accuracy of COSMO–RS model in predicting γ∞ of different solute families in various ILs based on a large experimental database. It was found that the AARDs between uncalibrated COSMO–RS predicted and experimental γ∞ differ significantly, ranging from 22.78% for thiophene to 207.93% for CCl4. To reduce systematic errors associated with this model, they calibrated the solute families, but the AARD still ranged from 19.23% for carboxylic acids to 56.80% for alkanes. Therefore, it is not suitable to use COSMO–RS predicted data generally in the UNIFAC–IL expansion process, especially for solute series with large AARDs. In view of this, they only generated a calculated pseudo-experimental database based on calibrated COSMO–RS predicted values with AARDs less than 30% for 7 solute families (i.e. alcohols, esters, aldehydes, nitroalkanes, thiophene, pyridine, and H2O) to specifically fill in the missing 72 parameters in the UNIFAC–IL parameter matrix. In addition to the activity coefficient method of COSMO-type, Chen et al. [32] also proposed to use ML-based models to generate pseudo-experimental data. They took advantage of the highly sparse feature of the currently available solute–IL γ∞ database and carefully developed a deep neural network-based RS to predict γ∞. The results showed that the obtained RS has high accuracy in predicting γ∞ for different solutes and solute families, outperforming calibrated COSMO–RS models and UNIFAC–IL models. Therefore, the establishment of a sparse experimental γ∞ database enabled the extended UNIFAC–IL model to cover all interaction parameters involved (the completed UNIFAC–IL model parameter matrix is shown in Figure 3.3). The application of γ∞ data obtained from the recommendation system to UNIFAC–IL extension is a good example of combining the advantages of ML and classical thermodynamic methods. It should be emphasized that the above UNIFAC–IL extensions all follow the framework of the original UNIFAC model. However, despite the widespread research and successful applications of the original UNIFAC model, it still has some limitations. For example, for certain strongly asymmetric systems, its predictions for γ∞, excess enthalpy (HE), and other aspects are not satisfactory. To overcome these weaknesses of the original UNIFAC model, Weidlich and Gmehling [43] proposed a modified UNIFAC model (also known as the Dortmund model) in 1987. The difference between the modified UNIFAC model and the original UNIFAC model lies in its unique combinatorial term and the introduction of temperature-dependent group interaction parameters and different van der Waals group parameters. These improvements make the Dortmund model more accurate in predicting the thermodynamic properties of certain specific systems. The modified UNIFAC model has also been extended to systems involving ILs. Figure 3.3 Extended UNIFAC–IL parameter matrix by combining experimental and neural recommender system predicted γ∞ data. Source: Chen et al. [32]/with permission of John Wiley & Sons. Kato and Gmehling [44] reported the extension of the modified UNIFAC model to IL-involved systems, especially the first extension to [RR′IM][BTI]. They introduced two main groups, imidazolium ([im]) and bis(trifluoromethanesulfonyl)imide ([BTI]–), and obtained their group interaction parameters with main groups such as alkanes, cycloalkanes, olefins, and alcohols by simultaneously fitting experimental VLE, γ∞, and HE data of related systems composed of different kinds of imidazolium cations and [BTI]– anions. In cases where the parameters were temperature-dependent, the modified UNIFAC model showed better consistency with experimental data than the original UNIFAC model in γ∞ and HE, while the deviation of the two models was similar in VLE. After this work, the same research group published a series of similar extensions covering 81 group interaction parameters in total [45–48]. Compared with the corresponding work of the original UNIFAC model, the modified UNIFAC model’s extension to IL-involved systems still covers a very limited number of groups. Therefore, obtaining more experimental data, especially temperature-related data such as VLE and HE, and further expanding the improved UNIFAC–IL model will be of great significance. This will enable us to predict the thermodynamic properties of complex systems involving ILs more accurately and promote the development of ILs and related fields. Another type of ML-based structure–property model is the ones built in a purely data-driven method. For instance, for one widely studied thermodynamic property of IL-involved systems, i.e. the solubility of carbon dioxide in ILs, Song et al. [49] reported two models by combining ML algorithms (ANN and SVM) with GC concepts. The model development employed a comprehensive dataset containing 10 116 solubility data of carbon dioxide in various ILs at different temperatures and pressures, with IL group, temperature, and pressure as model inputs. Based on an artificial-random hybrid strategy, the entire dataset was divided into a training set consisting of 8093 points and a test set consisting of 2023 points. Specifically, the least commonly used group’s data points were evenly divided into five folders, while all other data points were randomly distributed among the five folders. After training the model using four of the five folders, the estimated mean absolute error (MAE) and R2 for the ANN–GC model were 0.0202 and 0.9836, respectively, while the estimated MAE and R2 for the SVM–GC model were 0.0240 and 0.9783, respectively. Recently, DL algorithms have also been employed to predict the solubility of carbon dioxide in ILs. Chen et al. [30] extended the DL-based transformer–CNN framework to predict the solubility of CO2 in ILs (1 of the 11 benchmarks for validating the DL strategy). As only the SMILES representation of ILs, temperature, and pressure are required as inputs, and a rigorous 10-fold cross-validation procedure employing IL-based random dataset splitting strategies is utilized, the obtained model has a testing MAE of 0.022 and can thus be considered a valuable method for predicting CO2 solubility in ILs. The evolution and advancement of IL-related structure–property models, coupled with the assistance of ML methods, have sparked numerous initiatives in the computer-aided screening and design of ILs. These endeavors vary in their scope and approach, encompassing a range of properties and their interconnections, and can be broadly categorized into five groups: single-objective property screening, multilevel hierarchical screening, IL molecular design, sequential molecular design with process evaluation, and integrated molecular and process design. This spectrum covers diverse separation tasks, including LLE, ED, and gas absorption, as well as reaction separation processes like reactive extraction. Moreover, the realm of energy storage and conversion materials, such as heat transfer fluids, materials for solar energy storage, and electrolytes, has also been explored. In the following Sections 3.4.1, 3.4.2, 3.4.3, we will delve into exemplary applications of ML-facilitated IL screening and design, highlighting their varied uses in different application scenarios. The early availability of predictive thermodynamic methods such as COSMO–RS and COSMO–SAC has made it possible to assess various thermodynamic properties and has led to the screening of task-specific ILs for different separation tasks. The extraction of nitrogen and sulfur compounds from fuel oil, which is typically carried out to remove the final traces of these compounds, is an example of a solvent-sensitive system where the use of ILs as solvents in extraction systems can result in significant downstream issues or a significant decrease in fuel product quality. This means that even a small potential solubility of IL in the extract phase can result in significant downstream issues or a significant decrease in the fuel product quality. Therefore, special attention should be paid to this issue. A similar threat exists when ILs are used to separate organic compounds and metal ions from water mixtures, as well as to extract biopolymers or drugs. For these solvent-sensitive systems, Song et al. [50] proposed that, in addition to extraction capacity and selectivity, a strict criterion should be established to select suitable IL solvents for such systems, taking into account their solubility in the extract phase. To illustrate this point, they carried out a stepwise analysis of the influence of different anions, alkyl chain length, and the number of alkyl chains on the three thermodynamic parameters to screen ILs for desulfurization. Through COSMO–RS screening, a potential IL [Bmim][H2PO4] was successfully selected, which was then verified for its solubility in the extract phase and its extraction capacity through IL solubility, LLE, and multistage extraction experiments. The proposed solvent screening method was verified in the desulfurization process, and [Bmim][H2PO4] was selected through this screening method with its high extraction performance verified experimentally. Deodorizer distillate is a byproduct of vegetable oil refining and an important source of natural vitamin E. Qin et al. [51] used a combination of COSMO–RS prediction and experimental evaluation to screen for an IL that could be used as a carrier agent to extract natural vitamin E from deodorizer distillate (using a mixture of α-tocopherol and methyl linoleate as a model). First, COSMO–RS was used to study 47 different ILs with different anions based on the [Bmim] cation to identify the most promising candidate. The influence of alkyl chain length on the imidazole ring was also studied experimentally. It was found that the selectivity for vitamin E and the solubility of IL in methyl linoleate were directly proportional to the HB_acc3 descriptor factor of the anion. Taking into account the influence of the alkyl side chain length and number, [Hmim][OAc] was ultimately identified as the most promising IL, with a selectivity of 108.23 and a distribution coefficient of 8.18. Corn oil deodorization distillate was used as a model to verify its performance, which showed excellent performance in processing low concentrations of vitamin E. Following the establishment of these initial solvent selection frameworks tailored for specific process applications, numerous researchers have been actively adapting them. This includes the incorporation of various computational methods and models, along with adjustments to target characteristics to suit particular case studies. The separation of 1,3-butadiene (1,3-C4H6) and 1-butene (n-C4H8) presents a significant challenge due to their closely aligned boiling points and analogous molecular structures. ED is widely acknowledged as a viable method for this separation. In the context of ED processes, selecting an appropriate entrainer is of paramount importance. ILs have emerged as potential substitutes for traditional organic solvents, offering a pathway to reduce the energy consumption of these processes. Qin et al. [52] used COSMO–RS for high throughput computational screening of ILs, calculating the infinite dilution extraction capacity and selectivity of 36 260 ILs to find suitable entrainers. After screening, ILs that met preset thermodynamic criteria and physical property limitations were identified and subsequently sent for rigorous process simulation and design. It was found that 1,2,3,4,5-pentamethylimidazolium methyl carbonate was the best IL solvent. Compared to a benchmark ED process using the organic solvent N-methyl-2-pyrrolidone, energy consumption was reduced by 26%. To select suitable ILs as extraction solvents for industrial applications, Song et al. [53] proposed a systematic approach that combines COSMO–RS phase equilibrium calculations, GC model-based physical property predictions, and process simulation based on Aspen Plus to screen for practical ILs suitable for extraction. COSMO–RS can be used to predict the LLE of systems composed of the target mixture to be separated and different ILs, allowing for the pre-screening of ILs with higher mass distribution coefficients, stronger selectivity, and lower solvent losses. Then, the GC methods can be used to estimate the key physical properties of the pre-screened ion exchange resins, and further recommend candidate substances that meet certain physical property restrictions. Subsequently, the performance of the best candidate IL in a continuous process can be analyzed using Aspen Plus, and the optimal solvent based on the process can be ultimately determined. Taking the separation task as an example, a comprehensive hierarchical solvent screening framework can be developed by considering all important aspects from different studies, as shown in Figure 3.4. First, specific situations should be evaluated based on expert knowledge or database searches, such as potential solvent residues (losses), availability or synthetic accessibility, and reactivity with components in the system [54]. Subsequently, thermodynamic calculations based on COSMO models can be used to screen for IL candidates with satisfactory separation performance, such as phase equilibrium calculations, activity coefficient predictions, and Henry’s law constant calculations. In addition, important physical and EHS-related properties (e.g. melting point, viscosity, toxicity, and biodegradability) can be evaluated using empirical models or database searches to eliminate IL candidates that are unsuitable for practical applications, resulting in a shortlist of promising candidates. For these candidates, mechanism studies such as quantum chemical-based molecular interaction analysis or molecular dynamics simulations can be conducted to gain insights into their potential functions, while experiments can also be performed to verify their practical separation performance. Process simulations can be carried out in tools like Aspen Plus based on the pre-selected ILs to compare the process performance of different ILs. Finally, life cycle assessments (LCAs) can be conducted to carefully examine the environmental and sustainability impacts of IL-based processes. It should be noted that LCA, a common method for measuring the environmental impact of products during all stages of their life cycle, has some inherent limitations when applied to the IL field. Although further development is still needed, LCAs can serve as the final step in designing IL-based processes. For all the property estimations involved in the multilevel screening, ML models can be used wherever models are available or could be developed based on available databases. Figure 3.4 A multilevel hierarchical IL screening framework for separation tasks. Beyond the IL screening studies, there has been a surge in publications focused on IL design. These initial research efforts primarily concentrated on designing new IL molecular structures tailored to specific target properties or characteristics. For instance, leveraging the extension of GC–COSMO–SAC, Peng et al. [40] reported two CAILDs for separation processes, specifically the extraction of benzene from cyclohexane and the capture of carbon dioxide after combustion. They utilized the GC–COSMO–SAC model for estimating thermodynamic properties and applied semi-empirical models to approximate physical properties like melting point, viscosity, and surface tension. To address the mixed-integer nonlinear programming (MINLP) challenges in CAILD, a deterministic optimization strategy was employed, utilizing the branch and bound algorithm. Subsequently, further refinements were made to the GC–COSMO–SAC method, enabling the calculation of the σ-profile for the IL groups in its reference state, along with the introduction of two correction parameters (i.e. stretching and translation parameters). A framework for CAILD was proposed based on optimization, combining separation performance with penalties for violating physicochemical property and process requirement constraints as the objective function. To facilitate the use of the improved GC–COSMO–SAC model for thermodynamic property calculations, the IL was represented as a rooted tree, where each group was considered as a set of nodes connected by branches. To solve the CAILD problem based on optimization, they developed a mixed simulated annealing-genetic algorithm (MSAGA). The proposed CAILD framework was illustrated using two extraction processes, i.e. benzene/cyclohexane and heptane/thiophene, and ILs that have better separation performance than those reported in the literature were identified. This CAILD framework was subsequently extended to study different cases of carbon dioxide capture, i.e. flue gas (CO2/N2), syngas (CO2/H2), and acid gas (CO2/H2S), highlighting the importance of different design objectives. Finally, a recommendation was made for the absorption–selectivity–desorption index (ASDI) based on mass, which can effectively balance different ideal thermodynamic characteristics (i.e. gas solubility, selectivity, and desorption capacity) with low energy consumption. Zhang et al. [55] proposed a data-driven IL design strategy for carbon dioxide capture. They predicted carbon dioxide solubility using simpler and more reliable data-driven models instead of the traditional approach of combining state equations with the UNIFAC–IL model. Different batches of MINLP were based on multiple data-driven models trained from the same experimental database, and only ILs that were consistently identified across different batches were considered as reliable solutions within the effective domain of the data-driven model. The MINLP problem was encoded using GAMS27.2 and solved using the global optimization solver BARON. Through DFT calculations, the carbon dioxide capture performance of the designed ILs was ultimately confirmed, demonstrating that the proposed strategy can effectively improve design reliability. In many IL molecular design cases, different IL characteristics exhibit conflicting trends as molecular structures change, which makes selecting the best candidate substances a dilemma. The optimal method to balance the effects of different IL characteristics is through process simulation and evaluation because the best IL for a specific process application should be based on the highest process performance [27]. Therefore, several works on CAILD have included performing process studies after IL molecular design to make final selections from shortlists of pre-screened IL candidates. Song et al. [10] conducted a CAILD study on the extraction desulfurization of fuel oil. This study combined UNIFAC–IL extension, molecular design based on MINLP, and process evaluation based on Aspen Plus (as shown in Figure 3.5). First, they extended the UNIFAC–IL model to the extraction desulfurization system and proposed a MINLP problem based on it, with the objective function of maximizing the LLE performance of ILs. The constraints were imposed on structural feasibility and complexity, as well as thermodynamic and physical properties. The MINLP problem was solved using a generation-and-test method, gradually reducing the number of candidate ILs through different constraints, and finally, 44 candidate ILs were retained for target property evaluation. In a continuous extraction desulfurization process, the top five candidate ILs were evaluated, including an extraction tower and a distillation tower for IL regeneration. The results showed that all candidate ILs have much better process performance than the reference solvent sulfone. This CAILD framework was later extended by the research group to be used for n-hexane/methylcyclopentane ED, with different groups defined in the UNIFAC–IL extension to handle the proximity effects of groups in alkanes and cycloalkanes. Figure 3.5 Framework for CAILD by combining UNIFAC–IL extension, MINLP optimization, and process simulation. Source: Song et al. [10]/with permission of John Wiley & Sons. Wang et al. [56] combined molecular design of IL based on MINLP with TRNSYS simulation to identify candidate ILs that are promising as solar energy storage media and heat transfer fluids. The MINLP problem used a target function of thermal storage density, which integrated properties such as density, heat capacity, melting point, and decomposition temperature, while also considering physical property constraints such as thermal conductivity and viscosity. They solved the MINLP problem using the MSAGA mixed-integer algorithm and selected the top five IL molecules for TRNSYS simulation evaluation in long-term solar power generation systems. The results from annual system performance and long-term cost savings demonstrated the applicability, feasibility, and sustainability of the designed IL as a solar energy storage process medium. In summary, considering the best process performance in a specific process, both IL design and process configuration design are important. Although sequential IL molecular design and process evaluation can solve this issue to some extent, the intrinsic dependence of IL characteristics on process conditions cannot be fully addressed due to strong interactions between IL and process design. In fact, in most process evaluations, only a few ILs are typically retained, and the best-performing candidate ILs may be missed during the IL design step. Therefore, simultaneously solving both IL design and process design issues is highly desirable through integrated computer-aided ionic liquid and process design (CAILPD). Zhang et al. [57] reported a new method for integrated IL and absorption process design, where a rigorous rate-based process model is used to incorporate absorption thermodynamics and kinetics. They employed different types of models including GC models and thermodynamic models to predict the process-relevant physical, kinetic, and thermodynamic (gas solubility) properties of ILs. Combining the property models with the process models allows the integrated IL and process design problem to be formulated as an MINLP optimization problem. In the case study, the application of rigorous thermodynamic models (UNIFAC and PR) to predict the CO2 equilibrium solubility in ILs results in a convergence failure of the MINLP problem. To address this problem, they used an ANN-based surrogate model to replace the thermodynamic models, and successfully solved the integrated design problem to the global optimality. Although ILs have opened up a vast chemical space for chemical processes, selecting ILs with practical appeal for specific industrial applications can still be challenging. This is because, in many cases, only a small subset of ILs simultaneously meet multiple desired characteristics. For example, in the screening of ILs for fuel oil extractive desulfurization, only 831 candidates out of an initial set of 36 260 cation–anion combinations satisfy the thermodynamic property requirements. After imposing physical property constraints, only 15 candidates survive. It can be imagined that the number of viable candidates will further decrease if more restrictions such as commercial availability, ease of preparation, low cost, and EHS compatibility are taken into account. In some cases, there may not even be any candidates. Given this challenge, some researchers in the IL community have turned their attention to DSILs. Compared to classical two-ion ILs (i.e. one cation and one anion), DSILs consist of more than one cation and/or anion. Among different types of DSILs, [C1]x[C2]1−xA, C[A1]x[A2]1−x, and [C1A1]x[C2A2]1−x (see Figure 3.6) are more practical and convenient to be prepared. Considering the simplest way to obtain such DSILs is to mix different two-ion ILs together, they are often directly treated as IL mixtures in many cases. Rogers and coworkers [58] advocate the use of DSILs instead of IL mixtures because they found that IL mixtures behave differently from molecular mixtures: the ions in a single IL lose their identity and one cannot identify which ion comes from which IL; the properties of the mixtures arise from the properties of the ions and their relative proportions rather than the individual ILs used to make the mixture. Regardless of the terminology used, it is generally accepted that DSILs are more attractive than two-ion ILs in two aspects. First, DSILs greatly expand the chemical space for screening and designing process fluids. It is estimated that there are about 106 possible two-ion ILs, whereas only a few hundred have been synthesized or commercialized so far. In contrast, the potential DSILs that can be generated by simply mixing two-ion ILs can be much larger; even if only using commercialized or experimental ILs, a huge DSIL space can still be accessed. Second, DSILs are a convenient method for customizing desired properties. Typically, adjusting the properties of two-ion ILs involves changing alkyl chains and/or adding functional substituents; however, the synthesis and purification of these two-ion ILs (in many cases functional ILs) are always complicated, which greatly hinders their practical applications. On the contrary, adjusting the physical and thermodynamic properties of DSILs can be easily achieved by varying the characteristics and/or proportion of the parent ILs used for their preparation. Figure 3.6 Classical two-ion IL versus three common types of DSILs (C and A represent cation and anion, and x refers to the molar ion ratio). Although DSILs have opened up a new horizon for selecting process media, there have been relatively few studies on the computer-aided screening or design of DSILs compared to the research on ILs. Song et al. [59] reported the rational design of DSILs as extractants for the separation of thiophene/n-octane as an example. They first analyzed the influence of additional ions (cation/anion) and ion ratios on C∞ and S∞ through the COSMO–RS model, demonstrating them as important degrees of freedom in DSIL design. Three dependencies of C∞ on DSILs were observed (see Figure 3.7), and accordingly, DSILs were divided into three groups. In the first group, C∞ of DSILs monotonically change between the C∞ values of their IL parents; in the second and third groups, C∞ of DSILs show parabolic changes and display minimum and maximum values at certain ion ratios, respectively. They then performed multilevel screening of DSILs through predictions of infinite dilution thermodynamic properties, estimations of physical properties, assessments of phase equilibrium behavior, and experimental verification. It should be noted that since there are few QSPR models that can directly be used to evaluate Tm and η of DSILs, these two important physical properties were estimated based on the physical properties of their IL parents. Specifically, at least one of the IL parents in a DSIL should satisfy the Tm constraint condition, while η of the DSIL was estimated based on the molar average value of its IL parents. For the separation of thiophene/n-octane, [C2mim][OAc]x[SCN]1−x (x = [0.70, 1]). Figure 3.7 C∞ and S∞ of the representative DSILs as a function of the ion ratio x. Source: Song et al. [59]/with permission of John Wiley & Sons. Xie et al. [60] systematically investigated DSILs for the aromatics extraction from hydrocarbons (with o-xylene/n-octane as a model mixture) by combining a rational screening-validation of practical DSILs and a thorough microscopic mechanism exploration. They predicted key thermodynamic properties of paired DSILs from an initial pool of commercially available ILs by COSMO–RS and estimated the important physical properties of these ILs from those of corresponding parent ILs (retrieved from the experimental database or predicted by a DL model). The promising DSILs are followed up with LLE experimental tests, quantum chemistry calculation, and molecular dynamics simulation. The results of this work will be a valuable reference for guiding the design of DSILs for various applications. As introduced in this chapter, ML-boosted rational screening of task-specific ILs has been employed by numerous researchers to explore different applications. In the stage of structure–property modeling based on ML, it is necessary to adopt an appropriate molecular representation method, and different algorithms including classic linear and nonlinear methods as well as DL algorithms can be integrated. Apart from these two fundamental pillars, an ideal structure–property model is preferable to be built on a large model development dataset (to cover a large chemical space) and rigorous modeling procedures. However, many models cannot meet both requirements simultaneously, thus leading to a compromise between the design space of IL molecules and the reliability of the model when using the CAILD approach. As the optimal process medium should be determined based on the optimal process performance, an ideal design scenario would be the integrated design of IL molecules and process systems. Nevertheless, solving the correspondingly intricate mathematical problem poses a considerable challenge. Therefore, a trade-off has to be oftentimes made between the design space of IL molecules and the complexity of the model. When handling specific applications, people should consider existing models or models that can be endeavored based on available databases to select a pragmatic molecular design strategy. Irrespective of the approach adopted, the CAILD method can often save experimental costs and time, enabling the development of better processes based on selecting appropriate ILs as advanced process media. Despite the progress achieved thus far, there are still several future directions worth exploring. First, developing structure–property models that are more widely applicable or more accurate has always been a focus of attention, as few models satisfy both requirements simultaneously. These two aspects directly determine the chemical space that can be explored by CAILD and the reliability of the design results. Most CAILD studies must choose one or the other. To address this issue, additional data pools can be generated using theoretical tools such as quantum chemistry calculation; on the other hand, as ML methods become more prevalent and accessible, advanced data-driven methods are expected to play an increasingly important role. Second, most previous structural and property modeling efforts have mainly focused on basic physical properties and IL-related thermodynamic properties. Existing models for other important physical–chemical properties and EHS-related properties of ILs are either rare or limited to a small chemical space. This deficiency restricts the widespread application of CAILD in areas such as reaction solvents, energy storage media, and battery electrolytes among others. Moreover, as the mechanism of ILs in such applications is more complex, simulating such applications to formulate a CAILD problem still has a long way to go. Third, CAILD methods should be more closely integrated with experimental work to accelerate the practical application of ILs. A common challenge encountered by CAILD is that the best IL design may not be available commercially. In such cases, compromises often have to be made, and inferior but commercially available ILs are chosen for further testing, which are usually not as optimal as the designed candidates. This compromise not only leaves a gap in IL performance for the target process but also, in the long-term, hinders the development of IL structure–property models (as no data for new IL chemical space are obtained). Finally, as advanced ML methods for molecular property modeling (such as DNNs, CNNs, GNNs, and transformer) become more prevalent, how these models can be integrated within the CAILD framework and how the resultant problems can be effectively solved are worthwhile for future investigations.
3
Machine Learning-Aided Rational Screening of Task-Specific Ionic Liquids
3.1 Introduction
3.2 Molecule Representation of ILs
3.2.1 Groups or Fragment-Based Representation
3.2.2 COSMO-Derived Descriptors or Fingerprints
3.2.3 Machine-Learned Representations
3.3 Machine Learning-Based Structure–Property Models
3.3.1 Machine Learning for COSMO-Based Models
3.3.2 Machine Learning for UNIFAC Extensions
3.3.3 Pure Machine Learning Models
3.4 Applications
3.4.1 Computer-Aided IL Screening
3.4.2 Computer-Aided IL Design
3.4.3 Extensions to IL Mixtures
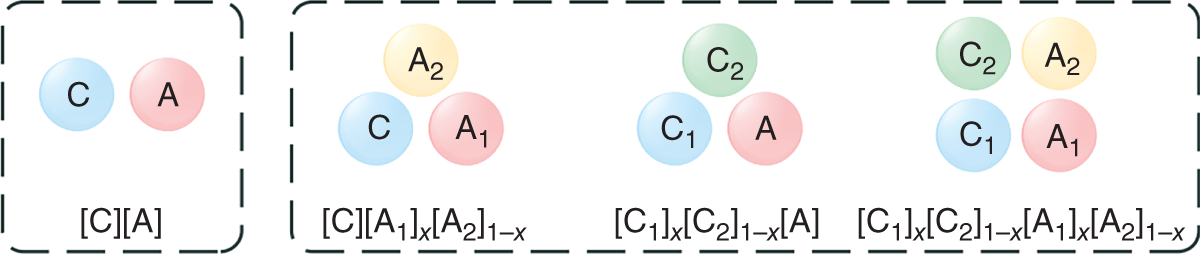
3.5 Conclusion and Perspectives
References