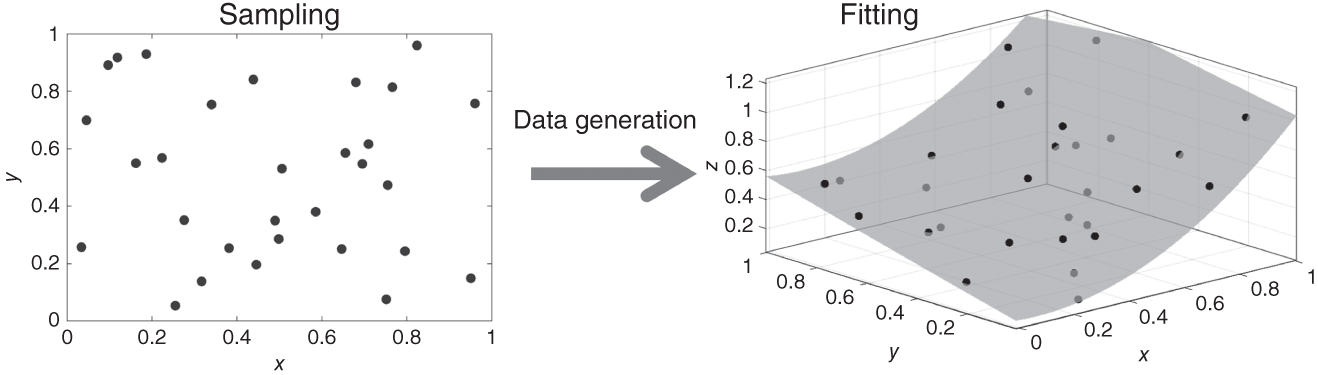
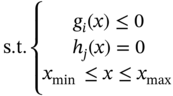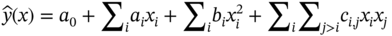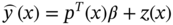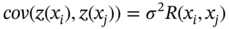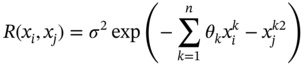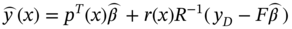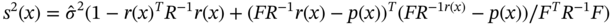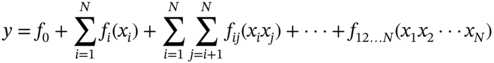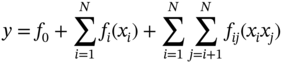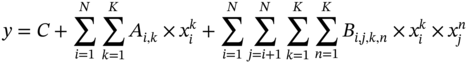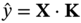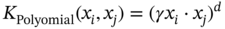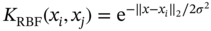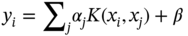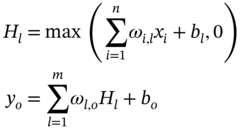Jianzhao Zhou1 and Jingzheng Ren1,2,3 1The Hong Kong Polytechnic University, Department of Industrial and Systems Engineering, Yuk Choi Road, Hong Kong SAR, China 2The Hong Kong Polytechnic University, Research Center for Resources Engineering Towards Carbon Neutrality, Yuk Choi Road, Kowloon, Hong Kong SAR, China 3The Hong Kong Polytechnic University, Research Institute for Advanced Manufacturing, Department of Industrial and Systems Engineering, Yuk Choi Road, Hung Hom, Kowloon, Hong Kong SAR, China Optimization in the field of chemical engineering plays a crucial role in improving process efficiency, reducing costs, ensuring product quality, enhancing safety, minimizing environmental impact, and supporting effective decision-making. It is an essential way to achieve environmentally friendly and economically viable chemical processes. The general form of optimization can be formulated as Eq. (10.1) [1]. The optimization problems are classified into different categories according to the type of variables (continuous and discrete optimization), the number of objective functions (single-objective and multi-objective optimization), the structure of equations (linear and nonlinear optimization), the availability of constraints (constrained optimization and unconstrained optimization), etc. where f is the evaluation function used to describe the relationship between the objective (obj) and the decision variables (x). g and f denote the inequality and equality constraints, respectively. The decision variables that appear in optimization can be continuous (temperature, pressure concentration, etc.) or discrete (number of plates in the distillation column, number of batches, etc.). The values of these variables are constrained to a range within the lower bound of xmin and the upper bound of xmax. Many contemporary optimization problems heavily rely on computer-based simulations, which offer accurate and useful paradigms for describing complex physical and chemical systems. While first-principle-based models, grounded in fundamental physical and chemical laws like the conservation of mass, momentum, and energy, provide crucial insights into system behavior, they present significant challenges in optimization, which can be seen as an inverse problem of simulation. In the domain of chemical engineering, these models, distinguished by their high-fidelity attributes, often assume a complex form, including non-algebraic equations, nonlinearities, and rigorous convergence [2]. For example, closed-circuit reverse osmosis (CCRO) systems typically entail the coupling of partial differential equations (PDEs) and ordinary differential equations (ODEs) [3]. Furthermore, flowsheet optimization problems are commonly displayed in the form of nonlinear programming characterized by nonconvexities and multiple local optima [4]. Even seemingly straightforward tasks, such as flash calculations, necessitate numerous iterations when the mechanism-based model is implemented [5]. In contrast, when dealing with a chemical reactor system involving multiple simultaneous reactions, each influenced by complex kinetics and thermodynamics, the computational requirements for modeling using first principles are exacerbated. This presents a challenge in optimization, resulting in prolonged simulation times and impeding the exploration of optimal operating conditions. Consequently, optimization-based on such mechanistic models becomes time-consuming and even infeasible in some cases, posing a persistent challenge despite substantial advancements in process systems engineering. Compounding the issue, a deterministic relationship between decision variables and their responses within an actual system remains unclear to researchers or engineers in certain scenarios [6]. To address the challenge of mechanism-based optimization, the surrogate modeling methodology that involves replacing costly or unclear model calls with computationally more affordable surrogate models can be employed. Essentially, the goal is to determine the alternative model to represent the mapping functions including, f, g, and h presented in Eq. (10.1). This approach has demonstrated its advantages and capabilities to provide accurate approximations of complex original models through surrogating (the surrogate models are also known as meta-models, regression surfaces, or emulators). Based on the available data from actual system operation or computationally intensive simulation, surrogate models can be constructed. Figure 10.1 presents a two-input surrogate model created by fitting 30 randomly sampled data points. The utilization of surrogate models can provide the following benefits: (i) a more efficient evaluation and compact description of the underlying input–output relationships, (ii) a more outstanding ability to integrate complex models from diverse sources, and (iii) increasing the speed of analyzing the design space and optimization process. As the volume of available data continues to grow, surrogate modeling becomes increasingly appealing for optimization implementation [7]. In chemical engineering, the utilization of surrogate models can be traced back to the mid-twentieth century. In 1951, George E. P. Box and K. B. Wilson employed a second-degree polynomial model to obtain an optimal response based on data from a sequence of designed experiments [8]. Though it was acknowledged that this model was only an approximation, such a model was easy to estimate and apply even with limited knowledge of the process or system. Subsequently, a series of surrogate models based on strategies such as order reduction [9] and machine learning [10] were proposed and applied in process optimization within the field of chemical engineering. Figure 10.1 An example of surrogate model construction. The basic workflow in surrogate modeling for optimization encompasses the following steps: (i) collect data from complex simulations or actual system operation of a chemical system, (ii) employ surrogate modeling techniques to construct surrogate models based on the available data, and (iii) assess the established surrogate model comprehensively and employ it in optimization. Among these steps, particular emphasis in this chapter will be placed on the construction of the surrogate model, considering its central role. Several characteristics of a given problem in the process influence its appropriateness for surrogacy, including linearity/nonlinearity, required accuracy, problem size (input dimensions), necessary information, computation speed, sample size, and the availability of convenient software or tools [11]. Section 10.2 introduces common surrogate models to guide selection, and Section 10.3 delves into the application specifics of surrogate modeling. Finally, Section 10.4 provides a concluding summary. Focusing on an exploration of surrogate modeling techniques opens the door to a diverse array of mathematical tools and algorithms designed to approximate the behavior of complex systems. Basically, surrogate modeling approaches can be categorized as interpolation (when the surrogate model aligns with the true function value at each point in the training dataset) or regression (when it does not) [12]. Initially, researchers primarily employed mathematical interpolation methods to establish surrogate models. Specifically, a series of system input and output data are used to establish the algebraic relationship between input and output variables through mathematical interpolation, gradually creating a mathematical model. Mature interpolation methods developed over time include Newton interpolation [13], spline interpolation [14], Lagrange interpolation [15], and Hermite interpolation [16]. The aforementioned interpolation method is relatively simple in mathematical structure and thus more computationally efficient, but the effect is generally moderate. Following this, researchers proposed the polynomial response surface model method to address the shortcomings of interpolation. Myers et al. [17] provided a detailed description of the polynomial response surface model, which utilizes mathematical polynomials of varying orders to characterize approximate models in engineering problems. The polynomial response surface model boasts a low computational cost, the ability to derive explicit mathematical expressions between system input and output variables, good continuity and differentiability, fast convergence speed, and ease of optimization. With the rapid development of artificial intelligence (AI)/machine learning, a large number of novel modeling techniques have emerged and been used in the construction of regression-based surrogate models, including but not limited to artificial neural networks (ANN), support vector machines (SVM), and decision trees (DT). While lacking explicit mathematical structure expressions, these models showcase remarkable fitting capabilities and have garnered significant attention. Each technique brings its unique strengths, tailored to capture specific aspects of system responses. This section introduces the most commonly used surrogate models in the literature related to optimization involved in chemical process engineering, including polynomial regression (PR), polynomial chaos expansion (PCE), Kriging, ANN, radial basis function (RBF), high-dimensional model representation (HDMR), SVM, and DT. Polynomial functions stand out as the predominant surrogate models in engineering applications [18]. Polynomials play a pivotal role in conveniently revealing the underlying relationship within chemical systems conveniently by leveraging the magnitudes of their coefficients to provide general insights into the design and optimization problem. They are recognized as one of the computationally simplest models for regression purposes and are recommended for less complex underlying models. Considering higher-order interactions often lack significance and demand more data to accommodate the additional parameters, quadratic polynomial functions, as surrogate models, are usually constrained to main effects and first-order interactions to approximate the relationship between decision variables and system response as outlined in Eq. (10.2) [6]. This simplified cutoff helps avoid overfitting, particularly when dealing with small datasets. where This class of regression models has a rich history in classical experimental design, particularly in scenarios where system information was frequently unknown. In such cases, it became imperative to devise methods capable of exploring the significance of the main process variables and their interactions as indicated by the determined coefficients [19]. Polynomial surrogates prove highly advantageous when coping with systems that exhibit a smooth response and thus are useful for continuous optimization. Higher efficiency is notable for low-dimensional problems. However, engineering practices often encounter high-dimensional and highly nonlinear systems. In such instances, polynomial surrogates may fall short of reliably representing the response surface [20, 21] and are usually restricted to local regions. PCE, also called Wiener chaos expansion [22], is a method for representing a random variable in terms of a polynomial function of other random variables. The selection of polynomials is based on their orthogonality with respect to the joint probability distribution of these random variables. This expansion offers a means to represent the response variable Y (seen as the random variable), with finite variance, as a function of an M-dimensional random vector X (decision variables). It employs a polynomial basis that is orthogonal to the distribution of this random vector. The standard form of PCE is given by the following equation [22]: where ci denotes coefficient to be determined and Ψi denotes a polynomial basis function. In the one-dimensional scenario, considering only the Gaussian distribution, the orthogonal polynomial basis functions are the set of ith degree Hermite polynomials Hi. The PCE of Y in terms of the standard random normal decision variables θi is expressed as follows [23]: The ith degree Hermite polynomials Hi can be defined as follows [23]: Since the polynomial chaos terms are functions of random variables, they become random variables, and terms of different orders are orthogonal to each other [24]. This orthogonality is defined in Gaussian measures as the expected value of the product of the two random variables. Due to the mean-square convergence of PCE, it is advantageous to calculate the coefficients using least-squares minimization (LSM), considering sample input/output pairs from the model. Optimization is carried out until the best fit is achieved between the surrogate PCE and the nonlinear model or simulated/experimental data. PCE has found applications in various domains such as electrical measurement, electric circuit models, chemical processes, biotechnological processes, reaction engineering, transport phenomena, batteries, robot manipulators, helicopters, and mechanical systems [23]. Kriging, with a mathematical basis as a Gaussian process regression (GPR) model [25], has emerged as a widely used method in surrogate modeling by capturing not only the mean response (expected value) but also the associated prediction uncertainty (variance). Originally developed to describe spatial distributions in geostatistics [26], Kriging gained popularity for deterministic computer experiments involving computationally demanding simulations [7, 27, 28]. Its flexibility in modeling various functions and interpolating data, along with the requirement for only a few fitted parameters, makes it a key technique among the surrogate modeling techniques. To achieve high performance in surrogating, as presented in Eq. (10.6), the model comprises a deterministic polynomial term representing the global trend of the data (pT(x)β) and a stochastic process accounting for the lack of fit in the polynomial term (z(x)) [29]. The stochastic part involves selecting a correlation function (Eq. (10.7)), either a priori or by fitting a semi-variogram to trends in the data. The Gaussian kernel function, also known as the squared-exponential or RBF kernel, is famous in the realm of chemical engineering due to its smoothness as presented in Eq. (10.8). Predictions for unsampled points are linear functions of observed data (Eq. (10.9)), and prediction errors are calculated using Eq. (10.10). Regions with high uncertainty in the sampling space can be identified, prompting the addition of new samples to enhance model performance. Kriging-specific adaptive sampling techniques have been developed to address this goal explicitly, as highlighted by various studies [20, 30, 31]. It is crucial to note that predictions assume the correct fitting of model parameters from observed data, and the predicted variance is itself a prediction of the expected model uncertainty. Kriging is recommended for problems with dimensions below 20, continuous variables, and smooth underlying functions [32]. In regression, discontinuities may lead to poor results due to the stationary covariance assumption of the correlation. Fitting the Kriging model (Eq. (10.9)) involves matrix inversion, becoming computationally demanding with large observed sets. There exist various types of Kriging beyond those presented here, and a comprehensive list of variants can be found in Yondo et al. [33]. RBFs is a powerful and versatile tool for approximating complex relationships between input and output variables. Belonging to the family of kernel-based methods, RBF is particularly well suited for applications in optimization, uncertainty quantification, and simulation of computationally expensive models. At its core, RBF leverages the concept of radial symmetry. It constructs a representation by combining local univariate functions, each centered around specific points, through a weighted linear combination [34]. This unique characteristic allows RBFs to efficiently capture complex and nonlinear patterns in data, enabling them especially effective in scenarios where the underlying relationships may be nonlinear or exhibit complex interactions. The RBF approximation takes the form of Eq. (10.10). This form of the RBF is identical to an ANN with a single hidden layer with RBFs [35]. Generally, RBF is applicable to situations where Kriging surrogates may be used, but are not as often used in chemical engineering modeling and optimization because the parameterized basis function of Kriging (which may be considered a special form of RBF) is preferred due to its higher accuracy, flexibility, and ability to make predictions of model variance [32]. Wang and Ierapetritou [36] recently addressed this issue by developing an adaptive sampling technique for cubic RBFs. In several cases, they showed that cubic RBFs improved flexibility in exploring the design space with higher accuracy while using fewer samples than Kriging. where xi denotes the ith center of n basis functions φ, which can take several forms; ‖x − xi‖2 evaluates the Euclidean distances between the prediction sites and the basis function centers; and λi are scalar weights during regression. HDMR stands out as an influential and efficient methodology employed in the generation of surrogate models. It has gained notable attention due to its exceptional precision in diverse industrial applications. HDMR’s distinctive capability lies in its feature of decomposing a comprehensive function into a summation of constituent functions, each represented by a specific subset of input variables. This intricate decomposition, as illustrated in Eq. (10.12), allows for an exact representation of the function under consideration. In practice, the application of HDMR proves pragmatic, as terms encompassing functions of more than two input parameters often contribute negligibly compared to lower-order terms [37, 38]. This truncated approximation, as presented in Eq. (10.13), remains not only efficient but also remarkably effective for a broad spectrum of models and datasets encountered in practical industrial settings. Though it is possible to evaluate each of these terms using direct numerical integration, a more efficient method is to approximate the functions fi and fij with analytic functions, as shown in Eq. (10.14) [39]. The truncated approximation provided by HDMR allows for flexibility in adjusting the model complexity based on the specific requirements of the problem and makes it possible to achieve the trade-off between accuracy and efficiency in surrogating [40]. As the dimensionality of the input space increases, the number of terms in the HDMR expansion grows exponentially. This can lead to challenges in terms of computational complexity and storage requirements, especially for large-scale systems. As PR, HDMR is more effective when dealing with smooth functions. where y is the calculated function value, N is the number of input variables, and f denotes the effect between input variables. C is a constant term, Ai,k and Bi,j,k,n are the first and second-order coefficients, K is the highest degree of input variables, and the subscripts i and j denote the ith and jth input parameters, respectively, while the subscripts k and n denote the orders of ith and jth input parameters. The decision tree is a powerful tool for capturing linear and nonlinear relationships in data and thus has great potential in surrogate modeling. In this context, decision tree surrogates undertake a process of recursive partitioning, systematically dividing the input space into distinct regions while assigning a constant value to each delineated region. In the pursuit of leveraging decision trees for surrogate modeling, the classification and regression tree (CART) algorithm emerges as a pivotal choice [41]. CART methodically constructs a binary tree structure, where internal nodes serve as splitting conditions predicated on input features, and leaf nodes stand as repositories for predicted class labels or continuous output values. The underpinning of CART lies in the application of linear regression to both parent and child nodes within the tree. The linear regression process, elucidated through Eqs. (10.15–10.19) [42], stands as a cornerstone in the CART methodology. These equations delineate the progression of linear regression across nodes, laying the groundwork for assessing the total variance (V), as depicted by a corresponding equation. This calculated total variance becomes instrumental in identifying the optimal division of the parent node, steering the decision tree toward a refined and data-informed structure. As a result, decision trees, with the CART algorithm at its core, offers a robust framework for constructing surrogate models that adeptly navigate nonlinearity, ensuring a precise representation of complex relationships within the underlying data. DT can be extended into ensemble methods like random forests, where multiple trees are combined to enhance predictive performance and reduce overfitting. One of the biggest challenges in using DT for surrogate modeling is the tendency of decision trees to overfit the training data, especially when the tree captures noise or specific patterns in the training data that do not generalize well to new, unseen data. This challenge arises due to the inherent flexibility of decision trees, which allows them to create complex, highly detailed structures to fit the training data perfectly [43]. where X is the matrix of model inputs, Y is the matrix of model outputs, K is the regression matrix, and SVM regression is a widely adopted and potent machine learning technique in surrogate modeling for optimization of chemical engineering systems, as evidenced by its successful applications in various industrial processes [44, 45]. SVM regression endeavors to determine a hyperplane within the feature space that maximizes the margin between data points and the hyperplane while minimizing regression errors. In the context of a training dataset comprising input vectors X = {x 1 , x 2 , …, xn} and corresponding target values y, SVM regression seeks to discover a regression function f(x) capable of accurately predicting the target variable for new input instances. In SVM regression, the polynomial kernel as defined by Eq. (10.20) [46] is frequently employed due to its advantageous combination of fast training and preservation of nonlinear capabilities [47]. It enables SVM regression to implicitly map features to a higher-dimensional space. Besides, Gaussian RBF kernel-based SVM, as shown in Eq. (10.21) [48] was recognized as the best choice for practical applications [49]. The objective of SVM regression is to find the optimal hyperplane that minimizes the regression error while satisfying the margin constraints. And the output (yi) can be predicted by Eq. (10.22). Although SVM regression is a robust and effective tool for surrogate modeling, offering high predictive accuracy and adaptability to complex relationships, its computational demands and sensitivity to certain parameters should be considered when applying it in practice. where γ is a scale factor, xi · xj denotes the dot product of the input vectors xi and xj. d is the polynomial degree. ‖x − xi‖2 indicates the Euclidean distances and σ is the width of the kernel in SVM. where αj and β are SVM parameters to be determined during training. ANN has emerged as a versatile and powerful machine learning approach, aiming to explore the complex relationships between input and output parameters. The essence of ANN lies in the composition of artificial neurons arranged in connected layers, where information is processed and transmitted [50]. These networks consist of units called artificial neurons, which receive numerical information from each neuron in the last layer and produce an analogous response forwarded to neurons in the subsequent layer. The transformative process involves weights assigned to each transmission, optimized during training using algorithms like backpropagation. This iterative optimization enables the model to learn and map input data to process responses, making ANN adept at representing diverse systems and yielding profound results across various tasks [51]. The capability of ANN to capture the global nature of design spaces for high-dimensional nonlinear systems is a distinct advantage. However, a key challenge lies in designing the appropriate network architecture, encompassing considerations such as layout, hyperparameters (e.g. learning rate, transfer functions, and regularization methods), and other intricate details. This process may require additional training and validation costs, demanding significant amounts of data to accommodate the large number of weights without overfitting. Figure 10.2 presents the topology structure of a typical three-layer ANN [42, 52]. Based on a rectified linear unit (ReLU)-activated hidden layer, which is widely used in modeling chemical systems [53], Eq. (10.23) shows the values of neurons in the hidden layer (Hl) are computed based on the values of neurons in the input layer (xi), which are subsequently employed in Eq. (10.24) to determine the output values (yo). The model’s parameters ω and b are determined by model training via the gradient descent optimization algorithm [54]. Figure 10.2 Schematic diagram of three-layer ANN. Source: [52]/with permission of Elsevier. where ωi,l indicates the connecting weight of ith node in the input layer and lth node in the hidden layer, bl represents the bias of lth node in the hidden layer, and n is the number of nodes in the input layer. Similarly, ωl,o denotes the connecting weight of lth node in the hidden layer and oth node in the output layer, while bo is the bias of oth node in the output layer, and m is the number of nodes in the hidden layer. In general, surrogate models of lower complexity that are inexpensive to evaluate and approximate accurately a large-scale model can greatly facilitate computationally intensive analysis tasks at hand. Such analysis specifically refers to optimizations, which are typically performed iteratively, or by relying on population-based algorithms. The prediction of surrogate models aids designers in performing optimization with an affordable number of computer simulations. Surrogate modeling has been widely used in the optimization and synthesis of chemical processes, which usually involves different units like reaction systems, separation systems, and heat exchange systems. Reaction engineering is a branch of chemical engineering that focuses on the design and optimization of chemical reactors and processes where chemical reactions occur. It encompasses the study of reaction kinetics, thermodynamics, and transport phenomena to understand and control chemical reactions within a chemical treatment step of a process. The primary objective is to design and operate reactors efficiently, ensuring optimal conversion of a variety of starting materials to desired products while considering performance indicators such as yield, selectivity, and safety. The application of surrogate models in accelerating the optimization of reactors can be classified based on the type of chemical reactors mainly including batch reactor, continuous stirred-tank reactor (CSTR), plug flow reactor, packed (fixed) bed reactor, fluidized bed reactor, membrane reactor, and microreactor. Batch processes, accounting for 40–60% of chemical process industries [55], such as those in food products, electronic chemicals, biotechnology, polymers, and pharmaceuticals [56], encounter challenges such as the absence of steady-state operating points, nonlinear behavior, constrained operation with limited measurements, and the presence of disturbances [57]. This complexity poses challenges for engineers in understanding and optimizing batch chemical reactors. To address these issues, Tasnim et al. [23] employed PCE to develop a nonlinear surrogate model of a batch chemical reaction process based on an assumed sequence reaction scheme. This surrogate model was subsequently used to identify the optimal temperature profile needed to maximize the concentration of an intermediate product at the end of the batch. Validation and optimization results demonstrated that the PCE-based surrogate model can be used as a robust approach for the rapid design, control, and optimization of batch reactor systems. Similarly, Kumar and Budman [58] utilized PCE in modeling a fed-batch bioreactor for robust optimization, showcasing its superior performance compared to its nominal counterparts. Besides, ANN was also widely used in modeling and trajectory optimization of a batch or a semibatch process [59]. Recently, Zhan et al. [60] compared the performances of PR and ANN in modeling co-digestion of poultry litter with wheat straw in an anaerobic sequencing batch reactor for biomethane production and then optimized the operational conditions for maximum methane yield based on the PR, which had better performance. ANN, as one of the most widely used surrogate models for CSTR [61, 62], was applied by Sivapathasekaran and Sen [63] to develop a nonlinear model for maximizing lipopeptide biosurfactant concentration using a genetic algorithm (GA). The plug flow reactor model is used to describe chemical reactions in continuous, flowing systems of cylindrical geometry based on certain assumptions. Significant work has been dedicated to surrogate modeling for such reactors. With data from a pilot-scale gasifier, reduced order model developed previously, Wang et al. [64] developed an ANN-based surrogate model, demonstrating its efficiency by being at least 4 orders of magnitude faster than reduced order models in optimizing operating conditions to achieve maximum carbon conversion and production of hydrogen gas. Simplifying the screening of input parameters, Jiang et al. [65] used HDMR in surrogate modeling for a rigorous kinetic-based plug flow reactor where hydrogen oxidation occurred to approximate the large system of ODE with simple algebraic equations to describe and solve the chemical kinetics. And then a deterministic global optimization method is used to optimize a hydrogen oxidation model using response surfaces obtained from the HDMR model. In addition, Shokry and Espuña [66] also used Kriging surrogate model to obtain simpler, accurate, robust, and computationally inexpensive predictive dynamic models for accelerating sequential dynamic optimization. Fixed bed reactors and fluidized bed reactors, commonly used in chemical engineering, are essential components whose modeling is of significant importance. Ayub and Zhou et al. [67, 68] have employed RBF-based surrogate optimization to achieve the best performance of a fluidized bed gasifier based on data from rigorous simulation and revealed the high efficiency of such an approach (with fast convergence during optimization). Regarding the optimization of gasification, Kim et al. [69] employed DT-based RF and ANN algorithms to construct a surrogate model to predict the outcomes of biomass gasification in a fluidized bed with high prediction accuracy. Additionally, Fang et al. [42] also developed decision tree and SVM as surrogate models for predicting the yield and profit of an industrial propane dehydrogenation process. This enables efficient optimization-based on particle swarm optimization, with the optimal solution typically found within the fifth to tenth generation of the optimization process. Notably, the datasets used for training these surrogate models are based on rigorous simulation. Regarding surrogate modeling for a member reactor, Waqas et al. [70] implemented the ANN and SVM to depict the statistical modeling approach using experimental datasets. Besides, SVM was also used to build the data-driven surrogate model of a microreactor based on computational fluid dynamic (CFD) simulation data and was further used to optimize the shape of the reactor [71]. To address the high computational complexity derived from CFD simulation, deep neural network-based surrogate modeling has also become a promising solution [72]. With abundant work focusing on this domain, surrogate modeling can be applied to optimize various aspects of these reactors, contributing to improved efficiency, selectivity, and overall process performance. Overall, ANN is one of the most widely used methods due to its high accuracy in modeling, while in comparison PR still exhibits a more apparent advantage in optimization efficiency due to its simple structure. Separation engineering, a specialized field within chemical engineering, focuses on the processes and methodologies involved in extracting components from mixtures to obtain pure substances. These separation processes are vital in various industries, including chemical manufacturing, pharmaceuticals, petrochemicals, and environmental engineering [73]. The goal is to efficiently isolate and purify specific substances from streams with complex mixtures, often involving physical or chemical methods. Typically, distillation is one of the most common techniques in separation engineering. Although rigorous distillation models are versatile and relatively accurate, ensuring convergence may necessitate good initial estimates. Additionally, their inherent computational complexity, like their discreteness in determining the plate number of columns, presents significant challenges when integrated into optimization frameworks. Recognizing its importance in chemical engineering, various surrogate modeling techniques have been explored for the optimization of distillation columns. Ibrahim et al. [74] have employed surrogate modeling to accelerate the optimization of crude oil distillation units. Their approach integrated surrogate models based on ANN with SVM to optimize column configuration and operating conditions. The SVM aided in filtering infeasible design options, reducing computational efforts, and enhancing the final solution’s quality. Rigorous process simulations and pinch analysis were employed to build the surrogate model and determine maximum heat recovery and minimum utility costs. To mitigate the nonlinearity and complexity of the integrated distillation optimization process, an RBF-based neural network was utilized as a surrogate model for function evaluation. This surrogate model helped to significantly reduce the computational expenses associated with the optimization process. Subsequently, efficient multi-objective optimization was achieved [75]. Besides, Quirante et al. used interpolation-based surrogate models like Kriging to obtain accurate models of distillation columns [76]. The surrogate-based optimization strategy ensures that convergence to a local optimum is guaranteed for numerical noise-free models. Kim et al. [77] used a computational-cost-efficient surrogate model based on machine learning, using data from a first-principle mathematical model implemented in the gPROMS® modeling environment [78]. The surrogate model considered adsorption pressure, desorption, feed rate, and rinse rate as input variables, successfully obtaining a Pareto front between productivity and purity in a vacuum pressure swing adsorption for CO separation process optimization. The input variables were determined as the adsorption pressure, desorption, feed rate, and rinse rate. Similar surrogate-based multi-objective optimization was also implemented by Beck et al. [79] to address the computational requirements of high-fidelity simulations needed to evaluate alternative designs. The study specifically employed the Kriging model due to its ability to generate confidence bands for predictions effortlessly. This outstanding advantage of the Kriging model facilitated effective navigation of the design space. Crystallization, another vital separation technique, separates components based on solubility differences. Surrogate models contribute to optimizing crystallization conditions, including temperature profiles, cooling rates, and seeding strategies, for improved yield and purity [80, 81]. It could be seen that in the realm of separation engineering, the surrogate model plays an important role in accelerating optimization, and a large number of techniques have shown satisfactory capabilities. Heat exchange, a fundamental process in thermodynamics and chemical engineering, involves transferring heat from one medium to another. Components like reboilers, condensers, and vaporizers, as the main heat exchangers, play key roles [82]. It is crucial for various industrial applications, such as power generation, refrigeration, and heating. Heat integration, on the other hand, refers to the systematic design and optimization of heat exchanger networks within a process to enhance energy efficiency. The goal of optimizing heat exchange and integration in chemical engineering is to minimize energy consumption, reduce utility costs, and improve overall process sustainability. Surrogate modeling has been employed in heat exchange and integration to optimize the design and operation of heat exchanger networks by a lot of researchers and engineers [83–85]. Typically, surrogate models have been utilized to optimize the selection and arrangement of heat exchangers within a network, involving determining the optimal number of stages, heat exchanger sizes, and their locations to maximize energy efficiency [86, 87]. In addition, numerous researches focus on the operating conditions of systems related to heat exchange and utilization. For example, Maakala et al. [88] employed the PR as a surrogate model to optimize the heat transfer performance of the recovery boiler superheaters with training data from CFD simulations. Furthermore, Zhou et al. [53] used linear regression and ANN in surrogate modeling organic Rankine cycle (ORC)-based combined system. The operations feasibility identification and energy prediction were achieved by surrogate models, and then the total efficiency optimization can be expressed as a mixed-integer linear programming (MILP) problem. Only ∼0.1 seconds is required, compared to more than 10 hours required for optimization based on the mechanistic model. Besides, Vilasboas et al. [89] used RF and PR for surrogate modeling of the ORC and used these established surrogate models to optimize the specific cost and energy efficiency of the ORC system. The results showed that the computational time was reduced by more than 99.9% for all indicated surrogates. These studies demonstrated that surrogate modeling poses great potential for accelerating the optimization of heat recovery and utilization systems by simplifying the mechanism-based model. The approach of employing surrogate modeling for various units involved in chemical processes, also known as surrogate-based superstructure optimization, enables the achievement of process design and synthesis with high efficiency [90]. As shown in Figure 10.3, the optimization-based “superstructure” methods for process synthesis are to determine the optimal pathways for conversion of feed to achieve the best performances in efficiency, economy, environment, etc. It is more powerful than traditional sequential-conceptual methods as they account for all complex interactions between design decisions. Palmer and Realff [91, 92] pioneered the optimization of chemical flow sheets using surrogates, employing PR and Kriging surrogates to handle limited datasets wisely. During the optimization, model reduction was conducted if insignificant input variables were identified. The results showed that this methodology yielded process configurations comparable to those reported in the literature. Davis and Ierapetritou [93] introduced one of the earliest surrogate-based optimization approaches, namely the Kriging-response surface methodology. This approach incorporated a sequential design method to model noisy black box functions within deterministic, feasible regions. Subsequently, they integrated a branch and bound method into the algorithm to handle integer variables, enabling the consideration of process synthesis and design problems [94]. In a follow-up article [95], discrete variables were incorporated directly into the black box models. Successful optimization of processes, including superstructures, such as purifying alcohol dehydrogenase and producing tert-butyl methacrylate, was achieved using Kriging models for the nonlinear programming (NLP) sub-problems. However, as the dimensionality of complete flow sheets increases, a modular or distributed approach becomes more practical. Henao and Maravelias [96] proposed a novel framework that achieved efficient superstructure optimization by simplifying formulation. The complex first-principle unit models were first replaced by compact and yet accurate ANN-based surrogate models and then binary variables that allow activation/deactivation of particular units were incorporated within the superstructure. Caballero and Grossmann [97] also applied surrogate models to replace individual units in a process flow sheet model, effectively lowering the dimensionality of each surrogate. In their study, they recommended a maximum dimensionality of 9 or 10 for each surrogate to prevent sampling from becoming the computationally limited step and to maintain surrogate accuracy. The choice of Kriging surrogate was motivated by its ability, at each iteration, to maintain the predicted variance of the model, facilitating convenient determination of stopping criteria and constraint feasibility. This allowed noise generated by simulation models to be considered as a stopping criterion for optimization. While this introduced higher computational costs for fitting and updating Kriging models compared to polynomials, the algorithm was explicitly designed not to update Kriging parameters at each iteration, aiming to generate satisfactory models initially with minimal adaptive improvement. Figure 10.3 Superstructure in chemical process engineering. The applicability of surrogate modeling has been demonstrated in practice. Recently, Quirante et al. [98] provided an example of using Kriging modeling in the successful superstructure optimization of a vinyl chloride monomer production process. Fahmi and Cremeschi [99] conducted a study on the superstructure optimization of a biodiesel plant, with ANN-based surrogates replacing each unit operation, thermodynamics, and mixing models. Notably, ANNs in several works were limited to simple network architectures with a single hidden layer and only a few neurons. Martino et al. [100] explored a feed-forward ANN-based superstructure optimization approach and showed the advantage of simple ANN (one layer and fewer nodes). While networks with simple structures are easy to fit and do not require large amounts of data, they lack the predictive power of larger networks. Larger networks require more data to prevent overfitting, which can become counterproductive when limited computational expense is desirable. With the development of deep learning represented by deep neural networks, more attention should be applied to building high-quality ANN when selected as a surrogate model, drawing insights from the machine learning community [51]. A notable case of surrogate modeling in superstructure optimization is the ALAMO framework [101], which designs mathematically simple surrogates from a set of basic functions using the least amount of data possible. Cozad et al. [102] added constrained regression to the method, placing bounds on the surrogate output to enhance extrapolation reliability, which is an important feature for modeling physical or safety limitations in chemical processes. ALAMO also holds the potential to achieve similar accuracy through adaptive sampling, which requires fewer data points compared to full sampling and thus reduces the number of complex simulations needed [103]. With a similar pattern, Boukouvala and Floudas [104] developed ARGONAUT, a framework for optimizing constrained global derivative-free optimization problems using surrogate models. Surrogates are automatically chosen from a list of possibilities (i.e. polynomials, RBF, Kriging) based on the need to limit complexity and maintain accuracy of the objective and constraints of the underlying gray-box models. Since process superstructure typically results in large-scale non-convex mixed-integer nonlinear programs (MINLP), which are very hard to solve effectively, surrogate modeling for the first-principle-based model has become more and more important. In most of the examples so far, the Gaussian process-based Kriging method has been implemented. However, with an increasing number of available data, ANN has become more popular in chemical engineering for process design and synthesis. Surrogate modeling has a huge advantage in simplifying the underlying relation involved in the study object and further reducing the computational burden for optimization. This chapter has provided an overview of the most commonly employed surrogate modeling techniques. The widespread adoption of these techniques, as highlighted in this discussion, has played a pivotal role in addressing challenging problems in chemical and process engineering. Due to the unremitting research and exploration of researchers, a large number of surrogate models have been successfully applied to accelerate the optimization of complex chemical systems. All of these efforts combine to establish a set of guidelines for surrogate model use and development. This, in turn, will lead to a more systematic and structured approach to surrogate modeling, enhancing the efficiency of modeling, optimizing, and studying complex processes. In the foreseeable future, with the development of AI, surrogate modeling coupled with cutting-edge AI methodologies holds promise for further accelerating the optimization of chemical processes. The authors express their sincere thanks to the Research Committee of The Hong Kong Polytechnic University for the financial support of the project through a PhD studentship (project account code: RKQ1). The work described in this paper was also supported by a grant from Research Grants Council of the Hong Kong Special Administrative Region, China-General Research Fund (Project ID: P0042030, Funding Body Ref. No: 15304222, Project No. B-Q97U) and a grant from Research Grants Council of the Hong Kong Special Administrative Region, China-General Research Fund (Project ID: P0046940, Funding Body Ref. No: 15305823, Project No. B-QC83).
10
Surrogate Modeling for Accelerating Optimization of Complex Systems in Chemical Engineering
10.1 Introduction
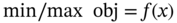
10.2 Surrogate Modeling Techniques
10.2.1 Polynomial Regression (PR)
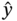 is the predicted response of the system, a, b, and c are the coefficients to be determined, while x is the decision variables and the subscripts i and j indicate the ith and jth decision variables, respectively.
is the predicted response of the system, a, b, and c are the coefficients to be determined, while x is the decision variables and the subscripts i and j indicate the ith and jth decision variables, respectively.
10.2.2 Polynomial Chaos Expansion


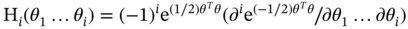
10.2.3 Kriging
10.2.4 Radial Basis Functions (RBF)
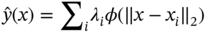
10.2.5 High-Dimensional Model Representation (HDMR)
10.2.6 Decision Tree (DT)
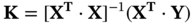
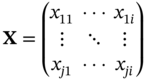
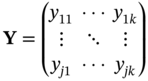
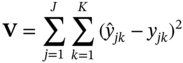
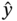 is the prediction matrix.
is the prediction matrix.
10.2.7 Support Vector Machine (SVM)
10.2.8 Artificial Neural Network (ANN)
10.3 Application of Surrogate Model in Optimization of Chemical Processes
10.3.1 Reaction Engineering
10.3.2 Separation Engineering
10.3.3 Heat Exchange and Integration
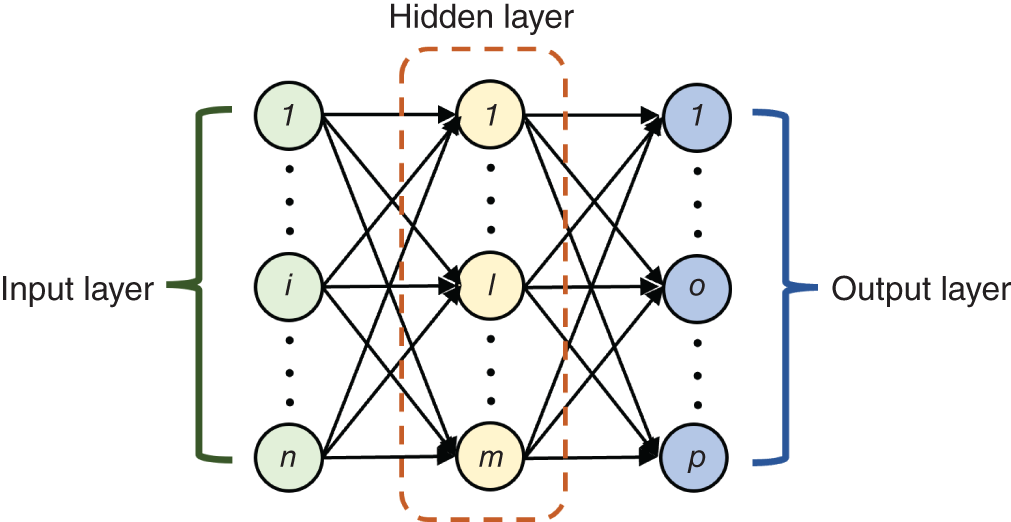
10.3.4 Process Design and Synthesis
10.4 Conclusion
Acknowledgment
References
Surrogate Modeling for Accelerating Optimization of Complex Systems in Chemical Engineering
(10.3)
(10.4)
(10.5)
(10.11)
(10.16)
(10.17)
(10.18)
(10.19)